In physics, spin is an intrinsic angular momentum associated with microscopic particles. It is a purely quantum mechanical phenomenon without any analogy in classical mechanics. Whereas classical angular momentum arises from the rotation of an extended object, spin is not associated with any rotating internal masses, but is intrinsic to the particle itself. Elementary particles such as the electron can have non-zero spin, even though they are believed to be point particles possessing no internal structure. The concept of spin was introduced in 1925 by Ralph Kronig , and independently by George Uhlenbeck and Samuel Goudsmit .
Properties of spin
As a quantum mechanical property, spin possesses a number of qualities that distinguish it from classical angular momentum. It is quantized, and can only take on discrete values. For instance, the spin angular momentum of an electron, measured along any particular direction, can only take on the values 
or 
(where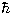 
is Planck's constant divided by 2π). Furthermore, the magnitude of the spin (a direction-independent quantity) is uniquely determined by the type of particle. Electrons are said to be "spin-half" particles, because the magnitude of every electron's spin is one half times 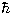. Other spin-half particles include neutrinos, protons, and neutrons. Photons are spin-one particles, and the hypothetical graviton is a spin-two particle. Certain exotic particles, such as pions, possess spin zero. The principles of quantum mechanics indicate that spin is restricted to integer or half-integer values, at least under normal conditions.
Mathematically, spin is not described by a vector, unlike classical angular momentum. It is described by objects known as spinors, which act differently from vectors under coordinate rotations.
It turns out that the spin of a particle is closely related to its properties in statistical mechanics. Particles with half-integer spin obey Fermi-Dirac statistics, and are known as fermions. They are subject to the Pauli exclusion principle, which forbids them from sharing quantum states, and are described in quantum theory by "antisymmetric states" (see the article on identical particles.) Particles with integer spin, on the other hand, obey Bose-Einstein statistics, and are known as bosons. These particles can share quantum states, and are described using "symmetric states". The proof of this is known as the spin-statistics theorem, which relies on both quantum mechanics and the theory of special relativity. In fact, the connection between spin and statistics is one of the most important and remarkable consequences of special relativity.
Particles with spin possess a magnetic moment, just like a rotating electrically charged body in classical physics. However, this magnetic moment exists even for point particles like the electron, and for electrically neutral particles like the neutron. This magnetic moment can be experimentally observed, by the deflection of particles by inhomogenous magnetic fields (as in the Stern-Gerlach experiment) or by the magnetic fields generated by the particles themselves. In fact, ferromagnetism arises from the alignment of the spins of the atoms in a solid.
Mathematical formulation of Spin ˝
The spin operator S behaves very much like L (angular momentum) where l = ˝. The spin operator has two eigenvalues: 
, which corresponds for two eigenstates — spin up and spin down. It is common to measure the spin in one direction — and the corresponding operator will be 
where n is a unit vector in the desired direction and
is the vectorial spin operator and the σ-s are Pauli matrices.
For example: Let's measure the spin in the z direction (in cartesian coordinates). Then Sz has two eigenstates — spin up and spin down. If we assign coordinates vectors as follow
then the corresponding operator in that representation will be
In the matrix representation, the operator acts on the coordinate vectors, often called "Spinors".
History
Wolfgang Pauli was possibly the most influential physicist in the theory of spin. Spin was first discovered in the context of the emission spectrum of alkali metals. In 1924 Pauli introduced what he called a "two-valued quantum degree of freedom" associated with the electron in the outermost shell. This allowed him to formulate the Pauli exclusion principle, stating that no two electrons can share the same quantum numbers.
The physical interpretation of Pauli's "degree of freedom" was initially unknown. Ralph Kronig , one of Landé 's assistants, suggested in early 1925 that it was produced by the self-rotation of the electron. When Pauli heard about the idea, he criticized it severely, noting that the electron's hypothetical surface would have to be moving faster than the speed of light in order for it to rotate quickly enough to produce the necessary angular momentum. This would violate the theory of relativity. Largely due to Pauli's criticism, Kronig decided not to publish his idea.
In the fall of that year, the same thought came to two young Dutch physicists, George Uhlenbeck and Samuel Goudsmit . Under the advice of Paul Ehrenfest, they published their results in a small paper. It met a favorable response, especially after L.H. Thomas managed to resolve a factor of two discrepancy between experimental results and Uhlenbeck and Goudsmit's calculations (and Kronig's unpublished ones). This discrepancy was due to the necessity to take into account the orientation of the electron's tangent frame, in addition to its position; mathematically speaking, a fiber bundle description is needed. The tangent bundle effect is additive and relativistic (i.e. it vanishes if c goes to infinity); it is one half of the value obtained without regard for the tangent space orientation, but with opposite sign. Thus the combined effect differs from the latter by a factor two (Thomas precession ).
Despite his initial objections to the idea, Pauli formalized the theory of spin in 1927, using the modern theory of quantum mechanics discovered by Schrödinger and Heisenberg. He pioneered the use of Pauli matrices as a representation of the spin operators, and introduced a two-component spinor wave-function.
Pauli's theory of spin was non-relativistic. However, in 1928, Paul Dirac published the Dirac equation, which described the relativistic electron. In the Dirac equation, a four-component spinor (known as a "Dirac spinor") was used for the electron wave-function.
In 1940, Pauli proved the spin-statistics theorem, which states that fermions have half-integer spin and bosons integer spin.
Magnetic material may be modelled by a system of spins located at positions in a lattice, where the interaction of neighboring spins contributes to the total energy of the system and the states of the spins change according to some non-deterministic (probabilistic) rule (the dynamics of the system). In the Ising model spins have only two possible states (up and down), whereas in the Potts model they may have more than two possible states. This is discussed in detail in Spin Models (http://www.hermetic.ch/compsci/thesis/chap1.htm), particularly in the section Modelling Magnetic Material (http://www.hermetic.ch/compsci/thesis/chap1.htm#s1.3) and subsequent sections.
Applications
Well established applications of spin are Magnetic Resonance Imaging or MRI, and GMR drive head technology in modern hard disks.
A possible application of spin is as a binary information carrier in spin transistors. Electronics based on spin transistors is called spintronics.
See also
References
