Planck's constant

Planck's constant, denoted h, is a physical constant that is used to describe the sizes of quanta. It plays a central role in the theory of quantum mechanics, and is named after Max Planck, one of the founders of quantum theory. It has a value of approximately

$h=6.626\ 069\ 3(11)\times10^{-34}\ \mbox{J}\cdot\mbox{s}$ .

With eV·s as energy unit:

$h=4.135\ 667\ 43(35)\ \times10^{-15} \mbox{eV}\cdot\mbox{s}$

Planck's constant has units of energy multiplied by time, which are the units of action. These units may also be written as momentum times distance (N·m·s), which are the units of angular momentum.

A closely-related quantity is the reduced Planck constant (sometimes called Dirac's constant):

$\hbar\equiv\frac{h}{2\pi}=1.054\ 571\ 68(18)\times10^{-34}\ \mbox{J}\cdot\mbox{s},$

where π is the constant pi. This constant is pronounced as "h-bar".

The figures cited here are the 2002 CODATA-recommended values for the constants and their uncertainties. The 2002 CODATA results were made available in December 2003 and represent the best-known, internationally-accepted values for these constants, based on all data available through 31 December 2002. New CODATA figures are scheduled to be published approximately every four years.

Planck's constant is used to describe quantization, a phenomenon occurring in microscopic particles such as electrons and photons in which certain physical properties occur in fixed amounts rather than assuming a continuous range of possible values. For instance, the energy E carried by a beam of light with constant frequency ν can only take on the values

$E = n h \nu \,,\quad n\in\mathbb{N}$

It is sometimes more convenient to use the angular frequency ω=2πν, which gives

$E = n \hbar \omega \,,\quad n\in\mathbb{N}$

Many such "quantization conditions" exist. A particularly interesting condition governs the quantization of angular momentum. Let J be the total angular momentum of a system with rotational invariance, and J_z the angular momentum measured along any given direction. These quantities can only take on the values

$\begin{matrix} J^2 = j(j+1) \hbar^2, & j = 0, 1/2, 1, 3/2, \ldots \\ J_z = m \hbar, \qquad\quad & m = -j, -j+1, \ldots, j\end{matrix}$

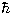Thus, $\hbar$ may be said to be the "quantum of angular momentum".

Planck's constant also occurs in statements of Heisenberg's uncertainty principle. The uncertainty (more precisely: the standard deviation) in any position measurement, Δx, and the uncertainty in a momentum measurement along the same direction, Δp, obeys

$\Delta x \Delta p \ge \begin{matrix}\frac{1}{2}\end{matrix} \hbar$

There are a number of other such pairs of physically measurable values which obey a similar rule.

On some browsers, the Unicode symbol ℎ (ℎ) is rendered as Planck's constant, and the symbol ℏ (ℏ) is rendered as Dirac's constant.

Reference

NIST link to CODATA value

Categories: Fundamental constants

The contents of this article are licensed from Wikipedia.org under the GNU Free Documentation License. How to see transparent copy

Encyclopedia

Dictionary

Quotes

Planck's constant

See also

Reference

The Online Encyclopedia and Dictionary

Encyclopedia

Dictionary

Quotes

Planck's constant

See also

Reference