(Redirected from
Phases of matter)
In the physical sciences, a phase is a set of states of a macroscopic physical system that have relatively uniform chemical composition and physical properties (i.e. density, crystal structure, index of refraction, and so forth.) The most familiar examples of phases are solids, liquids, and gases. Less familiar phases include plasmas and quark-gluon plasmas, Bose-Einstein condensates and fermionic condensates, strange matter, liquid crystals, superfluids and supersolids and the paramagnetic and ferromagnetic phases of magnetic materials.
Phases are sometimes called states of matter, but this term can lead to confusion with thermodynamic states. For example, two gases maintained at different pressures are in different thermodynamic states, but the same "state of matter".
Defining phases
Analyticity of the free energy
Although phases are conceptually simple, they are hard to define precisely. A good definition of a phase of a system is a region in the parameter space of the system's thermodynamic variables in which the free energy is analytic. Equivalently, two states of a system are in the same phase if they can be transformed into each other without abrupt changes in any of their thermodynamic properties.
All the thermodynamic properties of a system -- the entropy, heat capacity, magnetization , compressibility, and so forth -- may be expressed in terms of the free energy and its derivatives. For example, the entropy is simply the first derivative of the free energy with temperature. As long as the free energy remains analytic, all the thermodynamic properties will be well-behaved.
When a system goes from one phase to another, there will generally be a stage where the free energy is non-analytic. This is known as a phase transition. Familiar examples of phase transitions are melting (solid to liquid), freezing (liquid to solid), boiling (liquid to gas), and condensation (gas to liquid). Due to this non-analyticity, the free energies on either side of the transition are two different functions, so one or more thermodynamic properties will behave very differently after the transition. The property most commonly examined in this context is the heat capacity. During a transition, the heat capacity may become infinite, jump abruptly to a different value, or exhibit a "kink" or discontinuity in its derivative.
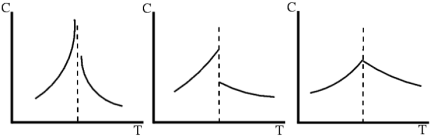
Possible graphs of heat capacity (C) against temperature (T) at a phase transition.
Relevant thermodynamic parameters
In practice, each type of phase is distinguished by a handful of relevant thermodynamic properties. For example, the distinguishing feature of a solid is its rigidity; unlike a liquid or a gas, a solid does not easily change its shape. Liquids are distinct from gases because they have much lower compressibility: a gas in a large container fills the container, whereas a liquid forms a puddle in the bottom. Many of the properties of solids, liquids, and gases are not distinct; for instance, it is not useful to compare their magnetic properties. On the other hand, the ferromagnetic phase of a magnetic material is distinguished from the paramagnetic phase by the presence of bulk magnetization without an applied magnetic field.
To take another example, many substances can exist in a variety of solid phases each corresponding to a unique crystal structure. These varying crystal phases of the same substance are called polymorphs. Diamond and graphite are examples of polymorphs of carbon. Graphite is composed of layers of hexagonally arranged carbon atoms, in which each carbon atom is strongly bound to three neighboring atoms in the same layer and is weakly bound to atoms in the neighboring layers. By contrast in diamond each carbon atom is strongly bound to four neighboring carbon atoms in a cubic array. The unique crystal structures of graphite and diamond are responsible for the vastly different properties of these two materials.
Metastable phases
Metastable states may sometimes be considered as phases, although strictly speaking they aren't because they are unstable. For example, each polymorph of a given substance is usually only stable over a specific range of conditions. For example, diamond is only stable at extremely high pressures. Graphite is the stable form of carbon at normal atmospheric pressures. Although diamond is not stable at atmospheric pressures and should transform to graphite, we know that diamonds exist at these pressures. This is because at normal temperatures the transformation from diamond to graphite is extremely slow. If we were to heat the diamond, the rate of transformation would increase and the diamond would become graphite. However, at normal temperatures the diamond can persist for a very long time.
Another important example of metastable polymorphs occurs in the processing of steel. Steels are often subjected to a variety of thermal treatments designed to produce various combinations of stable and metastable iron phases. In this way the steel properties, such as hardness and strength can be adjusted by controlling the relative amounts and crystal sizes of the various phases that form.
Phase diagrams
Main article: Phase diagram
The different phases of a system may be represented using a phase diagram. The axes of the diagrams are the relevant thermodynamic variables. For simple mechanical systems, we generally use the pressure and temperature. The following figure shows a phase diagram for a typical material exhibiting solid, liquid and gaseous phases.

A typical phase diagram.
The markings on the phase diagram show the points where the free energy is non-analytic. The open spaces, where the free energy is analytic, correspond to the phases. The phases are separated by lines of non-analyticity, where phase transitions occur, which are called phase boundaries.
In the above diagram, the phase boundary between liquid and gas does not continue indefinitely. Instead, it terminates at a point on the phase diagram called the critical point. This reflects the fact that, at extremely high temperatures and pressures, the liquid and gaseous phases become indistinguishable. In water, the critical point occurs at around 647 K (374 °C or 705 °F) and 22.064 MPa.
The existence of the liquid-gas critical point reveals a slight ambiguity in our above definitions. When going from the liquid to the gaseous phase, one usually crosses the phase boundary, but it is possible to choose a path that never crosses the boundary by going to the right of the critical point. Thus, phases can sometimes blend continuously into each other. We should note, however, that this does not always happen. For example, it is impossible for the solid-liquid phase boundary to end in a critical point in the same way as the liquid-gas boundary, because the solid and liquid phases have different symmetry.
An interesting thing to note is that the solid-liquid phase boundary in the phase diagram of most substances, such as the one shown above, has a positive slope. This is due to the solid phase having a higher density than the liquid, so that increasing the pressure increases the melting temperature. However, in the phase diagram for water the solid-liquid phase boundary has a negative slope. This reflects the fact that ice has a lower density than water, which is an unusual property for a material.
Emergence and universality
Phases are emergent phenomena produced by the self-organization of a macroscopic number of particles. Typical samples of matter, for example, contain around 1023 particles (on the order of Avogadro's number). In systems that are too small -- even, say, a thousand atoms -- the distinction between phases disappears, since the appearance of non-analyticity in the free energy requires a huge, formally infinite, number of particles to be present.
One might ask why real systems exhibit phases, since they are not actually infinite. The reason is that real systems contain thermodynamic fluctuations. When a system is far from a phase transition, these fluctuations are unimportant, but as it approaches a phase transition, the fluctuations begin to grow in size (i.e. spatial extent). At the ideal transition point, their size would be infinite, but before that can happen the fluctuations will have become as large as the system itself. In this regime, "finite-size" effects come into play, and we are unable to accurately predict the behavior of the system. Thus, phases in a real system are only well-defined away from phase transitions, and how far away it needs to be is dependent on the size of the system.
There is a corollary to the emergent nature of phase phenomena, known as the principle of universality. The properties of phases are largely independent of the underlying microscopic physics, so that the same types of phases arise in a wide variety of systems. This is a familiar fact of life. We know, for example, that the property that defines a solid -- resistance to deformation -- is exhibited by materials as diverse as iron, ice, and Silly Putty. The only differences are matters of scale. Iron may resist deformation more strongly than Silly Putty, but both maintain their shape if the applied forces are not too strong.
Phase separation
Different parts of a system may exist in different phases, in which case the phases are usually separated by boundary surfaces.
Gibbs' phase rule describes the number of phases that can be present at equilibrium for a given system at various conditions. The phase rule indicates that for a single component system at most three phases (usually gas, liquid and solid) can co-exist in equilibrium. The three phases can all co-exist only at a single specific temperature and pressure, characteristic of the material, called the triple point. The conditions where two phases become indistinguishable is called a critical point. The phase rule also indicates that two phases can only co-exist at equilibrium for specific combinations of temperature and pressure. For example for a liquid-gas system if the vapor pressure is lower than that corresponding to the temperature, the system will not be at equilibrium, rather the liquid will tend to evaporate until the vapor pressure reaches the appropriate level or all of the liquid is consumed. Likewise, if the vapor pressure is too great for the given temperature condensation will occur.
For the case of multi-component systems the phase rule indicates that additional phases are possible. A common example of this occurs in mixtures of mutually insoluble substances such as water and oil. If a few drops of oil are poured into pure water, there will be a small amount of intermixing, but there will be two distinct phases: one primarily oil and the other primarily water. The exact composition of the phases will be a function of the temperature and pressure but not a function of the amount of oil. It may be possible to change the temperature such that one of the phases disappears: for example, if the mixture is heated, it is possible that at some temperature, all of the oil is dissolved in the water. Above this temperature there is only one phase, and the composition of the phase does depend on how much oil was put in.
Phase separation can also exist in two dimensions. The boundaries between phases, the surfaces of materials, and the grain boundaries between different crystallographic orientations of a single material can also show distinct phases. For example, surface reconstructions on metal and semiconductor surfaces are two dimensional phases.
Links and references
External links
-
Science Daily, 2003-10-10: Metallic Phase For Bosons Implies New State Of Matter
-
2004-01-15, ScienceDaily: Probable Discovery Of A New, Supersolid, Phase Of Matter Citat: "...We apparently have observed, for the first time, a solid material with the characteristics of a superfluid...but because all its particles are in the identical quantum state, it remains a solid even though its component particles are continually flowing..."
-
2004-01-29, Sciencedaily: NIST/University Of Colorado Scientists Create New Form Of Matter: A Fermionic Condensate
-
French physicists find a solution that reversibly solidifies with a rise in temperature - α-cyclodextrine , water, and 4-methylpyridine
See also
Last updated: 05-13-2005 07:56:04