In linear algebra, the eigenvectors (from the German eigen meaning "inherent, characteristic") of a linear operator are non-zero vectors which, when operated on by the operator, result in a scalar multiple of themselves. The scalar is then called the eigenvalue associated with the eigenvector.
In applied mathematics and physics the eigenvectors of a matrix or a differential operator often have important physical significance. In classical mechanics the eigenvectors of the governing equations typically correspond to natural modes of vibration in a body, and the eigenvalues to their frequencies. In quantum mechanics, operators correspond to observable variables, eigenvectors are also called eigenstates, and the eigenvalues of an operator represent those values of the corresponding variable that have non-zero probability of occurring.
Examples
Intuitively, for linear transformations of two-dimensional space R2, eigenvectors are thus:
- rotation: no real valued eigenvectors. (Complex eigenvalue, eigenvector pairs exist).
- reflection: eigenvectors are perpendicular and parallel to the line of symmetry, the eigenvalues are -1 and 1, respectively
- uniform scaling: all vectors are eigenvectors, and the eigenvalue is the scale factor
- projection onto a line: eigenvectors with eigenvalue 1 are parallel to the line, eigenvectors with eigenvalue 0 are parallel to the direction of projection
Definition
Formally, we define eigenvectors and eigenvalues as follows: If A : V -> V is a linear operator on some vector space V, v is a non-zero vector in V and c is a scalar (possibly zero) such that
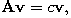
then we say that v is an eigenvector of the operator A, and its associated eigenvalue is c. Note that if v is an eigenvector with eigenvalue c, then any non-zero multiple of v is also an eigenvector with eigenvalue c. In fact, all the eigenvectors with associated eigenvalue c, together with 0, form a subspace of V, the eigenspace for the eigenvalue c.
Identifying eigenvectors
For example, consider the matrix
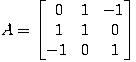
which represents a linear operator R3 -> R3. One can check that
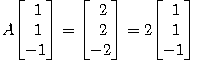
and therefore 2 is an eigenvalue of A and we have found a corresponding eigenvector.
The characteristic polynomial
An important tool for describing eigenvalues of square matrices is the characteristic polynomial: saying that c is an eigenvalue of A is equivalent to stating that the system of linear equations (A - cI) x = 0 (where I is the identity matrix) has a non-zero solution x (namely an eigenvector), and so it is equivalent to the determinant det(A - c I) being zero. The function p(c) = det(A - cI) is a polynomial in c since determinants are defined as sums of products. This is the characteristic polynomial of A; its zeros are precisely the eigenvalues of A. If A is an n-by-n matrix, then its characteristic polynomial has degree n and A can therefore have at most n eigenvalues.
Returning to the example above, if we wanted to compute all of A's eigenvalues, we could determine the characteristic polynomial first:
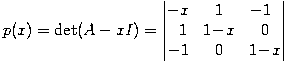
-
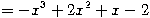
and because p(x) = - (x - 2)(x - 1)(x + 1) we see that the eigenvalues of A are 2, 1 and -1. The Cayley-Hamilton theorem states that every square matrix satisfies its own characteristic polynomial.
(In practice, eigenvalues of large matrices are not computed using the characteristic polynomial. Faster and more numerically stable methods are available, for instance the QR decomposition.)
Complex eigenvectors
Note that if A is a real matrix, the characteristic polynomial will have real coefficients, but not all its roots will necessarily be real. The complex eigenvalues will all be associated to complex eigenvectors.
In general, if v1, ..., vm are eigenvectors to different eigenvalues λ1, ..., λm, then the vectors v1, ..., vm are necessarily linearly independent.
The spectral theorem for symmetric matrices states that, if A is a real symmetric n-by-n matrix, then all its eigenvalues are real, and there exist n linearly independent eigenvectors for A which all have length 1 and are mutually orthogonal.
Our example matrix from above is symmetric, and three mutually orthogonal eigenvectors of A are
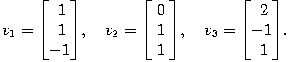
These three vectors form a basis of R3. With respect to this basis, the linear map represented by A takes a particularly simple form: every vector x in R3 can be written uniquely as
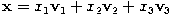
and then we have
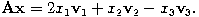
Infinite-dimensional spaces
The concept of eigenvectors can be extended to linear operators acting on infinite-dimensional Hilbert spaces or Banach spaces.
There are operators on Banach spaces which have no eigenvectors at all. For example, take the bilateral shift on the Hilbert space 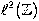 ; it is easy to see that any potential eigenvector can't be square-summable, so none exist. However, any bounded linear operator on a Banach space V does have non-empty spectrum. The spectrum σ(T) of the operator
; it is easy to see that any potential eigenvector can't be square-summable, so none exist. However, any bounded linear operator on a Banach space V does have non-empty spectrum. The spectrum σ(T) of the operator
T : V → V is defined as
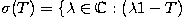 is not invertible
is not invertible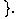
Then σ(T) is a compact set of complex numbers, and it is non-empty. When T is a compact operator (and in particular when T is an operator between finite-dimensional spaces as above), the spectrum of T is the same as the set of its eigenvalues.
The spectrum of an operator is an important property in functional analysis.
See also
External links