Mathematical formulation of quantum mechanics

One of the remarkable characteristics of the mathematical formulation of quantum mechanics, which distinguishes it from mathematical formulations of theories developed prior to the early 1900s, is its use of abstract mathematical structures, such as Hilbert spaces and operators on these spaces. Many of these structures had not even been considered before the twentieth century. In a general sense they are drawn from functional analysis, a subject within pure mathematics that developed in parallel with, and was influenced by the needs of quantum mechanics. In brief, physical quantities such as energy and momentum were no longer considered as functions on some phase space, but as operators on such functions.

This formulation of quantum mechanics continues to be used today, and still forms the basis of ab-initio calculations in atomic, molecular and solid-state physics. At the heart of the description is an idea of quantum state which, for systems of atomic scale, is radically different from the previous models of physical reality. While the mathematics is a complete description and permits calculation of many quantities that can be measured experimentally, there is a definite limit to access for an observer with macroscopic instruments. This limitation was first elucidated by Heisenberg through a thought experiment, and is represented mathematically by the non-commutativity of quantum observables.

Prior to the emergence of quantum mechanics as a separate theory, the mathematics used in physics consisted mainly of differential geometry and partial differential equations; probability theory was used in statistical mechanics. Geometric intuition clearly played a strong role in the first two and, accordingly, theories of relativity were formulated entirely in terms of geometric concepts. The phenomenology of quantum physics arose roughly between 1895 and 1915, and for the 10 to 15 years before the emergence of quantum theory (around 1925) physicists continued to think of quantum theory within the confines of what is now called classical physics, and in particular within the same mathematical structures. The most sophisticated example of this is the Sommerfeld-Wilson-Ishiwara quantization rule, which was formulated entirely on the classical phase space.

Contents

1 History of the formalism

1.1 The "old quantum theory" and the need for new mathematics
1.2 The "new quantum theory"
1.3 Later developments

2 Mathematical structure of quantum mechanics

2.1 Postulates of quantum mechanics
2.2 Pictures of dynamics
2.3 Representations
2.4 Time as an operator

3 The problem of measurement

3.1 Wavefunction collapse
3.2 The relative state interpretation

4 List of mathematical tools

History of the formalism

The "old quantum theory" and the need for new mathematics

Main article: Old quantum theory

In the decade of 1890, Planck was able to derive the blackbody spectrum and solve the classical ultraviolet catastrophe by making the unorthodox assumption that, in the interaction of radiation with matter, energy could only be exchanged in discrete units which he called quanta. Planck postulated a direct proportionality between the frequency of radiation and the quantum of energy at that frequency. The proportionality constant, h is now called Planck's constant in his honour.

In 1905, Einstein explained certain features of the photoelectric effect by assuming that Planck's light quanta were actual particles, which he called photons.

In 1913, Bohr calculated the spectrum of the hydrogen atom with the help of a new model of the atom in which the electron could orbit the proton only on a discrete set of classical orbits, determined by the condition that angular momentum was an integer multiple of Planck's constant. Electrons could make quantum leaps from one orbit to another, emitting or absorbing single quanta of light at the right frequency.

All of these developments were phenomenological and flew in the face of the theoretical physics of the time. Bohr and Sommerfeld went on to modify classical mechanics in an attempt to deduce the Bohr model from first principles. They proposed that, of all closed classical orbits traced by a mechanical system in its phase space, only the ones that enclosed an area which was a multiple of Planck's constant were actually allowed. The most sophisticated version of this formalism was the so-called Sommerfeld-Wilson-Ishiwara quantization . Although the Bohr model of the hydrogen atom could be explained in this way, the spectrum of the helium atom (classically an unsolvable 3-body problem) could not be predicted. The mathematical status of quantum theory remained uncertain for some time.

In 1923 de Broglie proposed that wave-particle duality applied not only to photons but to electrons and every other physical system.

The situation changed rapidly in the years 1925-1930, when working mathematical foundations were found through the groundbreaking work of Schrödinger and Heisenberg and the foundational work of von Neumann, Weyl and Paul Dirac, and it became possible to unify several different approaches in terms of a fresh set of ideas.

The "new quantum theory"

Schrödinger's wave mechanics originally was the first successful attempt at replicating the observed quantization of atomic spectra with the help of a precise mathematical realization of de Broglie's wave-particle duality. Schrödinger proposed an equation (now bearing his name) for the wave associated to an electron in an atom according to de Broglie, and explained energy quantization by the well-known fact that differential operators of the kind appearing in his equation had a discrete spectrum. However, Schrödinger himself initially did not understand the fundamental probabilistic nature of quantum mechanics, as he thought that the (amplitude squared) wavefunction of an electron must be interpreted as the charge density of an object smeared out over an extended, possibly infinite, volume of space. It was Max Born who introduced the probabilistic interpretation of the (amplitude squared) wave function as the probability distribution of the position of a pointlike object. With hindsight, Schrödinger's wave function can be seen to be closely related to the classical Hamilton-Jacobi equation.

Heisenberg's matrix mechanics formulation, introduced contemporaneously to Schrödinger's wave mechanics and based on algebras of infinite matrices, was certainly very radical in light of the mathematics of classical physics. In fact, at the time linear algebra was not generally known to physicists in its present form.

The reconciliation of the two approaches is generally associated to Paul Dirac, who wrote a lucid account in his 1930 classic Principles of Quantum mechanics. In it, he introduced the bra-ket notation, together with an abstract formulation in terms of the Hilbert space used in functional analysis, and showed that Schödinger's and Heisenberg's approaches were two different representations of the same theory. The first complete mathematical formulation of this approach is generally credited to von Neumann's 1932 book Mathematical Foundations of Quantum Mechanics, although Weyl had already referred to Hilbert spaces (which he called unitary spaces) in his 1927 classic book. It was developed in parallel with a new approach to the mathematical spectral theory based on linear operators rather than the quadratic forms that were David Hilbert's approach a generation earlier.

Though theories of quantum mechanics continue to evolve to this day, there is a basic framework for the mathematical formulation of quantum mechanics which underlies most approaches and can be traced back to the mathematical work of von Neumann. In other words, discussions about interpretation of the theory, and extensions to it, are now mostly conducted on the basis of shared assumptions about the mathematical foundations.

Later developments

The application of the new quantum theory to electromagnetism resulted in quantum field theory, which was developed starting around 1930. Quantum field theory has driven the development of more sophisticated formulations of quantum mechanics, of which the one presented here is a simple special case. In fact, the difficulties involved in implementing any of the following formulations cannot be said yet to have been solved in a satisfactory fashion except for ordinary quantum mechanics.

On a different front, von Neumann originally dispatched quantum measurement with his infamous postulate on the collapse of the wavefunction, raising a host of philosophical problems. Over the intervening 70 years, the problem of measurement became an active research area and itself spawned some new formulations of quantum mechanics.

Relative state/Many-worlds interpretation of quantum mechanics
Decoherence
Consistent histories formulation of quantum mechanics
Quantum logic formulation of quantum mechanics

A related topic is the relationship to classical mechanics. Any new physical theory is supposed to reduce to successful old theories in some approximation. For quantum mechanics, this translates into the need to study the so-called classical limit of quantum mechanics. Also, as Bohr emphasized, human cognitive abilities and language are inextricably linked to the classical realm, and so classical descriptions are intuitively more accessible than quantum ones. In particular, quantization, namely the construction of a quantum theory whose classical limit is a given and known classical theory, becomes an important area of quantum physics in itself.

Finally, some of the originators of quantum theory (notably Einstein and Schrödinger) were unhappy with what they thought were the philosophical implications of quantum mechanics. In particular, Einstein took the position that quantum mechanics must be incomplete, which motivated research into so-called hidden-variable theories. The issue of hidden variables has become in part an experimental issue with the help of quantum optics.

de Broglie-Bohm-Bell pilot wave formulation of quantum mechanics
Bell's inequalities
Kochen-Specker theorem

Mathematical structure of quantum mechanics

A physical system is generally described by three basic ingredients: states; observables; and dynamics (or law of time evolution) or, more generally, a group of physical symmetries . A classical description can be given in a fairly direct way by a phase space model of mechanics: states are points in a symplectic phase space, observables are real-valued functions on it, time evolution is given by a one-parameter group of symplectic transformations of the phase space, and physical symmetries are realized by symplectic transformations. A quantum description consists of a Hilbert space of states, observables are self-adjoint operators on the space of states, time evolution is given by a one-parameter group of unitary transformations on the Hilbert space of states, and physical symmetries are realized by unitary transformations.

Postulates of quantum mechanics

The following summary of the mathematical framework of quantum mechanics can be partly traced back to von Neumann's postulates.

Each physical system is associated with a separable complex Hilbert space H with inner product $\langle\phi\mid\psi\rangle$ . Rays (one-dimensional subspaces) in H are associated with states of the system. In other words, physical states can be identified with equivalence classes of vectors of length 1 in H, where two vectors represent the same state if they differ only by a phase factor. Separability is a mathematically convenient hypothesis, with the physical interpretation that countably many observations are enough to uniquely determine the state.
The Hilbert space of a composite system is the Hilbert space tensor product of the state spaces associated with the component systems. For a non-relativistic system consisting of a finite number of distinguishable particles, the component systems are the individual particles.
Physical symmetries act on the Hilbert space of quantum states unitarily or antiunitarily (supersymmetry is another matter entirely).
Physical observables are represented by densely-defined self-adjoint operators on H.

The expected value (in the sense of probability theory) of the observable A for the system in state represented by the unit vector $\left|\psi\right\rangle\in H$ is

$\langle\psi\mid A\mid\psi\rangle$

By spectral theory, we can associate a probability distribution to the values of A in any state ψ. We can also show that the possible values of the observable A in any state must belong to the spectrum of A. In the special case A has discrete spectrum, the possible values of A in any state are its eigenvalues.

More generally, a state can be represented by a so-called density operator, which is a trace class, nonnegative self-adjoint operator

ρ

normalized to be of trace 1. The expected value of A in the state

ρ

$\operatorname{tr}(A\rho)$

ρ ψ

is the orthogonal projector onto the one-dimensional subspace of H spanned by $\left|\psi\right\rangle$ , then

$\operatorname{tr}(A\rho_\psi)=\left\langle\psi\mid A\mid\psi\right\rangle$

Density operators are those that are in the closure of the convex hull of the one-dimensional orthogonal projectors. Conversely, one-dimensional orthogonal projectors are extreme points of the set of density operators. Physicists also call one-dimensional orthogonal projectors pure states and density operators mixed states.

One can in this formalism state Heisenberg's uncertainty principle and prove it as a theorem, although the exact historical sequence of events, concerning who derived what and under which framework, is the subject of historical investigations outside the scope of this article.

Superselection sectors. The correspondence between states a rays needs to be refined somewhat to take into account so-called superselection sectors . States in different superselection sectors cannot influence each other, and the relative phases between them are unobservable.

Pictures of dynamics

In the so-called Schrödinger picture of quantum mechanics, the dynamics is given as follows:

The state is given by a differentiable map (with respect to the Hilbert space norm topology) from time, which is an infinite one dimensional manifold parameterized by t, to the Hilbert space of states. If $\left|\psi\left(t\right)\right\rangle$ denotes the state of the system at any one time t, the following Schrödinger equation holds:

$i\hbar\frac{d}{dt}\left|\psi(t)\right\rangle=H\left|\psi(t)\right\rangle$

where H is a densely-defined self-adjoint operator, called the system Hamiltonian, i is the imaginary unit and 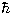$\hbar$ is the reduced Planck constant. As an observable, H corresponds to the total energy of the system.

Alternatively, one can state that there is a continuous one-parameter unitary group U(t): H → H such that

$\left|\psi(t+s)\right\rangle=U(t)\left|\psi(s)\right\rangle$

for all times s, t. The existence of a self-adjoint Hamiltonian H such that

$U(t)=e^{-(i/\hbar)t H}$

is a consequence of Stone's theorem on one-parameter unitary groups.

The Heisenberg picture of quantum mechanics focuses on observables and instead of considering states as varying in time, it regards the states as fixed and the observables as changing. To go from the Schrödinger to the Heisenberg picture one needs to define time-independent states and time-dependent operators thus:

$\left|\psi\right\rangle = \left|\psi(0)\right\rangle$

$A(t) = U(-t)AU(t) \quad$

It is then easily checked that the expected values of all observables are the same in both pictures

$\langle\psi\mid A(t)\mid\psi\rangle=\langle\psi(t)\mid A\mid\psi(t)\rangle$

and that the time-dependent Heisenberg operators satisfy

$i\hbar{d\over dt}A(t) = [A(t),H]$

This assumes A is not time dependent in the Schrödinger picture.

The so-called Dirac picture or interaction picture has time-dependent states and observables, evolving with respect to different Hamiltonians. This picture is most useful when the evolution of the states can be solved exactly, confining any complications to the evolution of the operators. For this reason, the Hamiltonian for states is called "free Hamiltonian" and the Hamiltonian for observables is called "interaction Hamiltonian". In symbols:

$i\hbar\frac{\partial}{\partial t}\left|\psi(t)\right\rangle=\operatorname{H_0}\left|\psi(t)\right\rangle$

$i\hbar{\partial\over\partial t}A(t) = [A(t),H_{\rm int}]$

The interaction picture does not always exist, though. In interacting quantum field theories, Haag's theorem states that the interaction picture does not exist. This is because the Hamiltonian cannot be split into a free and an interacting part within a superselection sector.

The Heisenberg picture is the closest to classical mechanics, but the Schrödinger picture is considered easiest to understand by most people, to judge from pedagogical accounts of quantum mechanics. The Dirac picture is the one used in perturbation theory, and is specially associated to quantum field theory.

Similar equations can be written for any one-parameter unitary group of symmetries of the physical system. Time would be replaced by a suitable coordinate parameterizing the unitary group (for instance, a rotation angle, or a translation distance) and the Hamiltonian would be replaced by the conserved quantity associated to the symmetry (for instance, angular or linear momentum).

Representations

The original form of the Schrödinger equation depends on choosing a particular representation of Heisenberg's canonical commutation relations. The Stone-von Neumann theorem states all irreducible representations of the finite-dimensional Heisenberg commutation relations are unitarily equivalent. This is related to quantization and the correspondence between classical and quantum mechanics, and is therefore not strictly part of the general mathematical framework.

The quantum harmonic oscillator is an exactly-solvable system where the possibility of choosing among more than one representation can be seen in all its glory. There, apart from the Schrödinger (position or momentum) representation one encounters the Fock (number) representation and the Bargmann-Segal (phase space or coherent state) representation. All three are unitarily equivalent.

Time as an operator

The framework presented so far singles out time as the parameter that everything depends on. It is possible to formulate mechanics in such a way that time becomes itself an observable associated to a self-adjoint operator. At the classical level, it is possible to arbitrarily parameterize the trajectories of particles in terms of an unphysical parameter s, and in that case the time t becomes an additional generalized coordinate of the physical system. At the quantum level, translations in s would be generated by a "Hamiltonian" H-E, where E is the energy operator and H is the "ordinary" Hamiltonian. However, since s is an unphysical parameter, physical states must be left invariant by "s-evolution", and so the physical state space is the kernel of H-E (this requires the use of a rigged Hilbert space and a renormalization of the norm).

This is related to quantization of constrained systems and quantization of gauge theories.

The problem of measurement

The picture given in the preceding paragraphs is sufficient for description of a completely isolated system. However, it fails to account for one of the main differences between quantum mechanics and classical mechanics, that is the effects of measurement.

Wavefunction collapse

When von Neumann proposes his mathematical postulate for quantum mechanics he included the following "measurement postulate".

Carrying out a measurement of an observable A with discrete spectrum on a system in the state represented by $\left|\psi\right\rangle$ will cause the system state to collapse into an eigenstate (i.e. eigenvector), $\left|\psi_a\right\rangle$ of the operator; the observed value corresponds to the eigenvalue a of the eigenstate:

$A \left|\psi_a\right\rangle=a\left|\psi_a\right\rangle$

Mathematically, the collapse corresponds to orthogonal projection of $\left|\psi\right\rangle$ onto the eigenspace of A corresponding to the observed value a

Von Neumann's postulate regarding the effects of measurement has always been a source of confusion and speculation. Fortunately, there is a general mathematical theory of such irreversible operations (see quantum operation) and various physical interpretations of the mathematics.

The relative state interpretation

An alternative interpretation of measurement is Everett's relative state interpretation, which was later dubbed "many-worlds interpretation" of quantum mechanics.

List of mathematical tools

Part of the folklore of the subject concerns the mathematical physics textbook Courant-Hilbert, put together by Richard Courant from David Hilbert's Göttingen University courses. The story is told (by mathematicians) that physicists had dismissed the material as not interesting in the current research areas, until the advent of Schrödinger's equation. At that point it was realised that the mathematics of the new quantum mechanics was already laid out in it. It is also said that Heisenberg had consulted Hilbert about his matrix mechanics, and Hilbert observed that his own experience with infinite-dimensional matrices had derived from differential equations, advice which Heisenberg ignored, missing the opportunity to unify the theory as Weyl and Dirac did a few years later. Whatever the basis of the anecdotes, the mathematics of theory was conventional at the time, where the physics was radically new.

The main tools include:

Categories: Quantum mechanics

Last updated: 05-13-2005 07:56:04

Encyclopedia

Dictionary

Quotes

Mathematical formulation of quantum mechanics

History of the formalism