Categories: Differential geometry | Differential topology | Order theory | Abstract algebra

Embedding

In mathematics, an embedding (or imbedding) is one instance of some mathematical object contained within another instance, such as a group that is a subgroup.

Contents

1 Topology/Geometry

1.1 General topology
1.2 Differential geometry
1.3 Riemannian geometry

2 Algebra

2.1 Field Theory

3 Domain theory

4 See also

Topology/Geometry

General topology

In general topology, an embedding is a homeomorphism onto its image. More explicitly, a map f : X → Y between topological spaces X and Y is an embedding if f yields a homeomorphism between X and f(X) (where f(X) carries the subspace topology inherited from Y). Intuitively then, the embedding f : X → Y lets us treat X as a subspace of Y. Every embedding is injective and continuous. Every map that is injective, continuous and either open or closed is an embedding; however there are also embeddings which are neither open nor closed. The latter happens if the image f(X) is neither an open set nor a closed set in Y.

Differential geometry

In differential geometry: Let M and N be smooth manifolds and 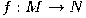$f:M\to N$ be a smooth map, it is called an immersion if for any point 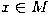$x\in M$ the differential 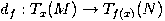$d_f:T_x(M)\to T_{f(x)}(N)$ is injective (here $T x (M)$ denotes tangent space of $M$ at $x$ ). Then an embedding, or a smooth embedding, is defined to be an immersion which is an embedding in the above sense (i.e. homeomorphism onto its image). When the manifold is compact, the notion of a smooth embedding is equivalent to that of an injective immersion.

In other words, an embedding is diffeomorphic to its image, and in particular the image of an embedding must be a submanifold. An immersion is a local embedding (i.e. for any point 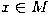$x\in M$ there is a neighborhood 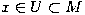$x\in U\subset M$ such that $f:U\to N$ is an embedding.)

An important case is N=Rⁿ. The interest here is in how large n must be, in terms of the dimension m of M. The Whitney embedding theorem states that n = 2m is enough. For example the real projective plane of dimension 2 requires n = 4 for an embedding. The less restrictive condition of immersion applies to the Boy's surface—which has self-intersections.

Riemannian geometry

In Riemannian geometry: Let (M,g) and (N,h) be Riemannian manifolds. An isometric embedding is a smooth embedding f : M → N which preserves the metric in the sense that g is equal to the pullback of h by f, i.e. g = f*h. Explicitly, for any two tangent vectors

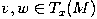
$v,w\in T_x(M)$

we have

g (v, w) = h (d f (v), d f (w))

Analogously, isometric immersion is an immersion between Riemannian manifolds which preserves the Riemannian metrics.

Equivalently, an isometric embedding (immersion) is a smooth embedding (immersion) which preserves length of curves (cf. Nash embedding theorem).

Algebra

Field Theory

In field theory, an embedding of a field E in a field F is a ring homomorphism σ : E → F.

The kernel of σ is an ideal of E which cannot be the whole field E, because of the condition σ(1)=1. Therefore the kernel is 0 and thus any embedding of fields is a monomorphism. Moreover, E is isomorphic to the subfield σ(E) of F. This justifies the name embedding for an arbitrary homomorphism of fields.

Domain theory

In domain theory, an embedding of partial orders is F in the function space [X → Y] such that

For all x₁, x₂ in X, x₁ ≤ x₂ if and only if F (x₁) ≤ F(x₂) and
For all y in Y, {x : F (x) ≤ y } is directed.

Based on an article from FOLDOC, used by permission.

Encyclopedia

Dictionary

Quotes

Embedding